SEMrun() converts a (directed, undirected, or mixed)
graph to a SEM and fits it. If a binary group variable (i.e., case/control)
is present, node-level or edge-level perturbation is evaluated.
This function can handle loop-containing models, although multiple
links between the same two nodes (including self-loops and mutual
interactions) and bows (i.e., a directed and a bidirected link between
two nodes) are not allowed.
Usage
SEMrun(
graph,
data,
group = NULL,
fit = 0,
algo = "lavaan",
start = NULL,
SE = "standard",
n_rep = 1000,
limit = 100,
...
)Arguments
- graph
An igraph object.
- data
A matrix whith rows corresponding to subjects, and columns to graph nodes (variables).
- group
A binary vector. This vector must be as long as the number of subjects. Each vector element must be 1 for cases and 0 for control subjects. If
NULL(default), group influence will not be considered.- fit
A numeric value indicating the SEM fitting mode. If
fit = 0(default), no group effect is considered. Iffit = 1, a "common" model is used to evaluate group effects on graph nodes. Iffit = 2, a two-group model is used to evaluate group effects on graph edges.- algo
MLE method used for SEM fitting. If
algo = "lavaan"(default), the SEM will be fitted using the NLMINB solver fromlavaanR package, with standard errors derived from the expected Fisher information matrix. Ifalgo = "ricf", the model is fitted via residual iterative conditional fitting (RICF; Drton et al. 2009), with standard error derived from randomization or bootstrap procedures. Ifalgo = "cggm", model fitting is based on constrained Gaussian Graphical Modeling (CGGM), with DAG nodewise Lasso procedure and de-biasing asymptotic inference (Jankova & Van De Geer, 2019).- start
Starting value of SEM parameters for
algo = "lavaan". If start isNULL(default), the algorithm will determine the starting values. If start is a numeric value, it will be used as a scaling factor for the edge weights in the graph object (graph attributeE(graph)$weight). For instance, a scaling factor is useful when weights have fixed values (e.g., 1 for activated, -1 for repressed, and 0 for unchanged interaction). Fixed values may compromise model fitting, and scaling them is a safe option to avoid this problem. As a rule of thumb, to our experience,start = 0.1generally performs well with (-1, 0, 1) weights.- SE
If "standard" (default), with
algo = "lavaan", conventional standard errors are computed based on inverting the observed information matrix. If "none", no standard errors are computed.- n_rep
Number of randomization replicates (default = 1000), for permutation flip or boostrap samples, if
algo = "ricf".- limit
An integer value corresponding to the network size (i.e., number of nodes). Beyond this limit, the execution under
algo = "lavaan"will run withSE = "none", iffit = 0, or will be ridirected toalgo = "ricf", iffit = 1, or toalgo = "cggm", iffit = 2. This redirection is necessary to reduce the computational demand of standard error estimation by lavaan. Increasing this number will enforce lavaan execution whenalgo = "lavaan".- ...
Currently ignored.
Value
A list of 5 objects:
"fit", SEM fitted lavaan, ricf, or cggm object, depending on the MLE method specified by the
algoargument;"gest" or "dest", a data.frame of node-specific ("gest") or edge-specific ("dest") group effect estimates and P-values;
"model", SEM model as a string if
algo = "lavaan", andNULLotherwise;"graph", the induced subgraph of the input network mapped on data variables. Graph edges (i.e., direct effects) with P-value < 0.05 will be highlighted in red (beta > 0) or blue (beta < 0). If a group vector is given, nodes with significant group effect (P-value < 0.05) will be red-shaded (beta > 0) or lightblue-shaded (beta < 0);
"data", input data subset mapping graph nodes, plus group at the first column (if no group is specified, this column will take NA values).
Details
SEMrun maps data onto the input graph and converts it into a
SEM. Directed connections (X -> Y) are interpreted as direct causal
effects, while undirected, mutual, and bidirected connections are
converted into model covariances. SEMrun output contains different sets
of parameter estimates. Beta coefficients (i.e., direct effects) are
estimated from directed interactions and residual covariances (psi
coefficients) from bidirected, undirected, or mutual interactions.
If a group variable is given, exogenous group effects on nodes (gamma
coefficients) or edges (delta coefficients) will be estimated.
By default, maximum likelihood parameter estimates and P-values for
parameter sets are computed by conventional z-test (= estimate/SE),
and fits it through the lavaan function, via
Maximum Likelihood Estimation (estimator = "ML", default estimator in
lavOptions).
In case of high dimensionality (n.variables >> n.subjects), the covariance
matrix could not be semi-definite positive and thus parameter estimates
could not be done. If this happens, covariance matrix regularization
is enabled using the James-Stein-type shrinkage estimator implemented
in the function pcor.shrink of corpcor R package.
Argument fit determines how group influence is evaluated in the
model, as absent (fit = 0), node perturbation (fit = 1),
or edge perturbation (fit = 2). When fit = 1, the group
is modeled as an exogenous variable, influencing all the other graph
nodes. When fit = 2, SEMrun estimates the differences
of the beta and/or psi coefficients (network edges) between groups.
This is equivalent to fit a separate model for cases and controls,
as opposed to one common model perturbed by the exogenous group effect.
Once fitted, the two models are then compared to assess significant
edge (i.e., direct effect) differences (d = beta1 - beta0).
P-values for parameter sets are computed by z-test (= d/SE), through
lavaan. As an alternative to standard P-value
calculation, SEMrun may use either RICF (randomization or bootstrap
P-values) or GGM (de-biased asymptotically normal P-values) methods.
These algorithms are much faster than lavaan
in case of large input graphs.
References
Pearl J (1998). Graphs, Causality, and Structural Equation Models. Sociological Methods & Research., 27(2):226-284. <https://doi.org/10.1177/0049124198027002004>
Yves Rosseel (2012). lavaan: An R Package for Structural Equation Modeling. Journal of Statistical Software, 48(2): 1-36. <https://www.jstatsoft.org/v48/i02/>
Pepe D, Grassi M (2014). Investigating perturbed pathway modules from gene expression data via Structural Equation Models. BMC Bioinformatics, 15: 132. <https://doi.org/10.1186/1471-2105-15-132>
Drton M, Eichler M, Richardson TS (2009). Computing Maximum Likelihood Estimated in Recursive Linear Models with Correlated Errors. Journal of Machine Learning Research, 10(Oct): 2329-2348. <https://www.jmlr.org/papers/volume10/drton09a/drton09a.pdf>
Jankova, J., & Van De Geer, S (2019). Inference in high-dimensional graphical models. In Handbook of Graphical Models (2019). Chapter 14 (sec. 14.2): 325-349. Chapman & Hall/CRC. ISBN: 9780429463976
Hastie T, Tibshirani R, Friedman J. (2009). The Elements of Statistical Learning (2nd ed.). Springer Verlag. ISBN: 978-0-387-84858-7
Grassi M, Palluzzi F, Tarantino B (2022). SEMgraph: An R Package for Causal Network Analysis of High-Throughput Data with Structural Equation Models. Bioinformatics, 38 (20), 4829–4830 <https://doi.org/10.1093/bioinformatics/btac567>
See also
See fitAncestralGraph and fitConGraph
for RICF algorithm and constrained GGM algorithm details, respectively.
Author
Mario Grassi mario.grassi@unipv.it
Examples
#### Model fitting (no group effect)
sem0 <- SEMrun(graph = sachs$graph, data = log(sachs$pkc))
#> NLMINB solver ended normally after 10 iterations
#>
#> deviance/df: 66.93938 srmr: 0.0894911
#>
summary(sem0$fit)
#> lavaan 0.6-20 ended normally after 10 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 30
#>
#> Number of observations 1766
#>
#> Model Test User Model:
#>
#> Test statistic 2409.815
#> Degrees of freedom 36
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> zAkt ~
#> zPIP3 -0.065 0.020 -3.251 0.001
#> zPKA 0.546 0.020 27.454 0.000
#> zErk ~
#> zMek -0.021 0.021 -0.974 0.330
#> zPKA 0.456 0.021 21.506 0.000
#> zJnk ~
#> zPKA 0.093 0.024 3.940 0.000
#> zPKC 0.128 0.024 5.439 0.000
#> zMek ~
#> zPKA 0.011 0.018 0.615 0.539
#> zPKC -0.006 0.017 -0.321 0.748
#> zRaf 0.683 0.018 38.931 0.000
#> zP38 ~
#> zPKA -0.018 0.018 -0.988 0.323
#> zPKC 0.646 0.018 35.504 0.000
#> zPIP2 ~
#> zPIP3 0.489 0.020 24.698 0.000
#> zPlcg 0.227 0.020 11.441 0.000
#> zPKC ~
#> zPIP2 0.020 0.025 0.782 0.434
#> zPlcg 0.014 0.025 0.570 0.568
#> zPlcg ~
#> zPIP3 0.207 0.023 8.895 0.000
#> zRaf ~
#> zPKA -0.124 0.024 -5.261 0.000
#> zPKC -0.037 0.024 -1.587 0.113
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> zPIP3 ~~
#> zPKA -0.103 0.024 -4.306 0.000
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .zAkt 0.690 0.023 29.715 0.000
#> .zErk 0.790 0.027 29.715 0.000
#> .zJnk 0.973 0.033 29.715 0.000
#> .zMek 0.534 0.018 29.715 0.000
#> .zP38 0.583 0.020 29.715 0.000
#> .zPIP2 0.663 0.022 29.715 0.000
#> .zPKC 0.999 0.034 29.715 0.000
#> .zPlcg 0.957 0.032 29.715 0.000
#> .zRaf 0.982 0.033 29.715 0.000
#> zPIP3 0.999 0.034 29.715 0.000
#> zPKA 0.999 0.034 29.715 0.000
#>
head(parameterEstimates(sem0$fit))
#> lhs op rhs est se z pvalue ci.lower ci.upper
#> 1 Akt ~ PIP3 -0.065 0.020 -3.251 0.001 -0.104 -0.026
#> 2 Akt ~ PKA 0.546 0.020 27.454 0.000 0.507 0.585
#> 3 Erk ~ Mek -0.021 0.021 -0.974 0.330 -0.062 0.021
#> 4 Erk ~ PKA 0.456 0.021 21.506 0.000 0.415 0.498
#> 5 Jnk ~ PKA 0.093 0.024 3.940 0.000 0.047 0.139
#> 6 Jnk ~ PKC 0.128 0.024 5.439 0.000 0.082 0.174
# Graphs
gplot(sem0$graph, main = "significant edge weights")
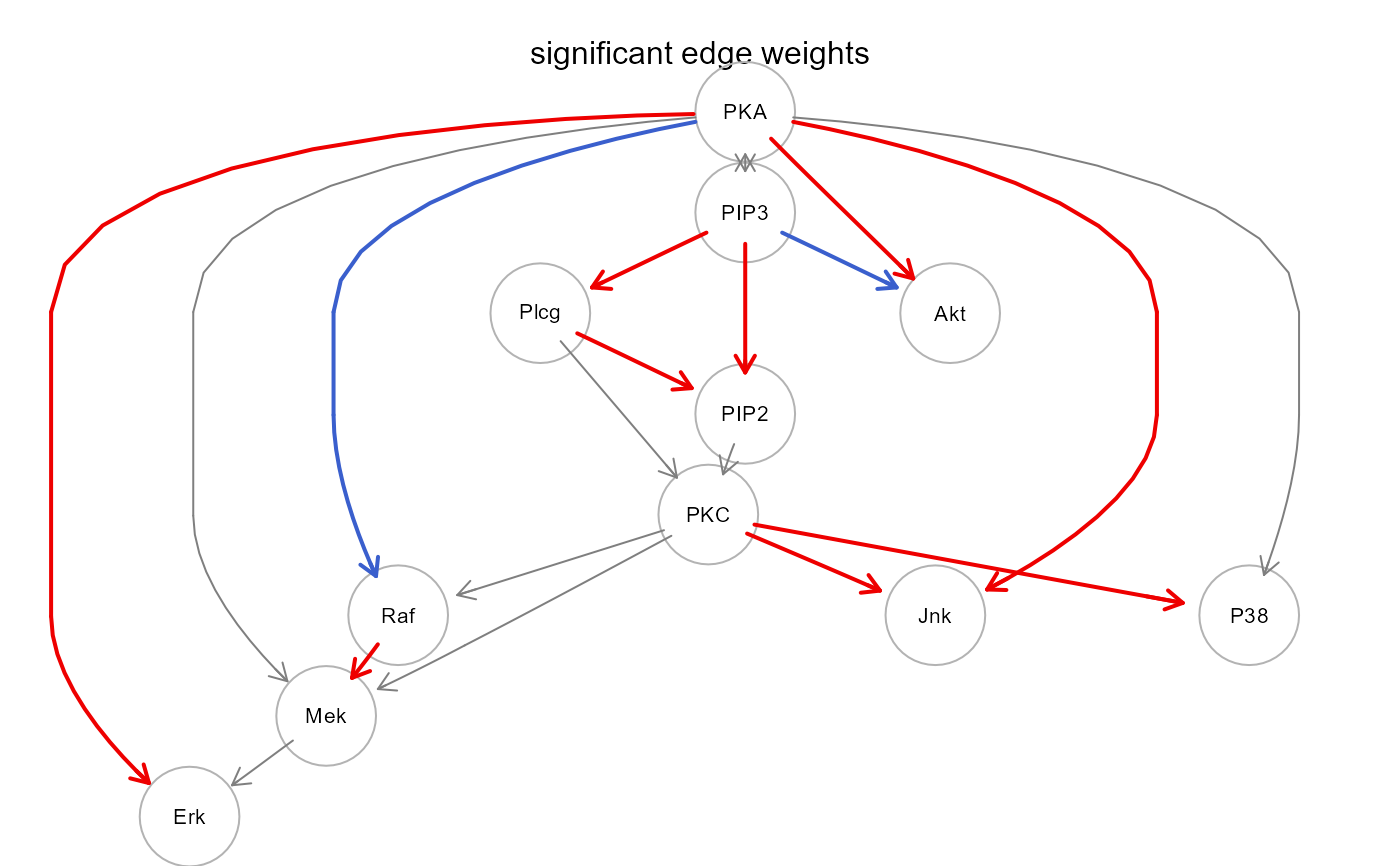 plot(sem0$graph, layout = layout.circle, main = "significant edge weights")
plot(sem0$graph, layout = layout.circle, main = "significant edge weights")
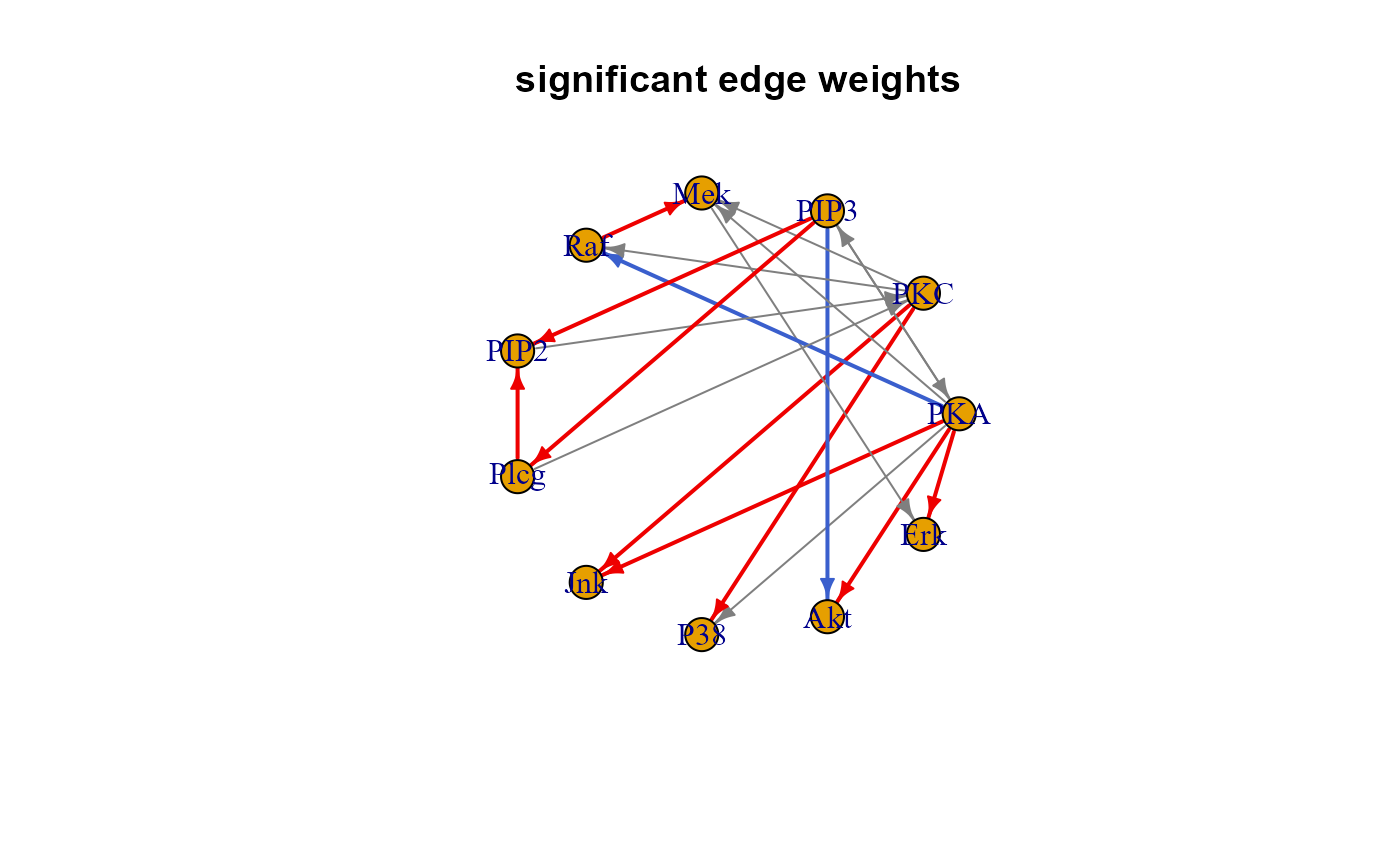 #### Model fitting (common model, group effect on nodes)
sem1 <- SEMrun(graph = sachs$graph, data = log(sachs$pkc),
group = sachs$group)
#> NLMINB solver ended normally after 5 iterations
#>
#> deviance/df: 61.84444 srmr: 0.0701161
#>
#> Brown's combined P-value of node activation: 2.664535e-15
#>
#> Brown's combined P-value of node inhibition: 0.2368274
#>
# Fitting summaries
summary(sem1$fit)
#> lavaan 0.6-20 ended normally after 5 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 41
#>
#> Number of observations 1766
#>
#> Model Test User Model:
#>
#> Test statistic 2226.396
#> Degrees of freedom 36
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> zAkt ~
#> group 0.150 0.021 7.057 0.000
#> zErk ~
#> group 0.179 0.022 8.046 0.000
#> zJnk ~
#> group 0.333 0.023 14.279 0.000
#> zMek ~
#> group 0.122 0.020 6.036 0.000
#> zP38 ~
#> group -0.062 0.019 -3.274 0.001
#> zPIP2 ~
#> group 0.110 0.021 5.243 0.000
#> zPIP3 ~
#> group -0.301 0.023 -13.278 0.000
#> zPKA ~
#> group 0.290 0.023 12.720 0.000
#> zPKC ~
#> group 0.116 0.024 4.818 0.000
#> zPlcg ~
#> group 0.268 0.024 11.359 0.000
#> zRaf ~
#> group -0.467 0.022 -21.080 0.000
#> zAkt ~
#> zPIP3 -0.023 0.020 -1.148 0.251
#> zPKA 0.507 0.020 24.859 0.000
#> zErk ~
#> zMek 0.016 0.021 0.748 0.454
#> zPKA 0.407 0.022 18.760 0.000
#> zJnk ~
#> zPKA -0.002 0.023 -0.080 0.936
#> zPKC 0.096 0.022 4.284 0.000
#> zMek ~
#> zPKA -0.017 0.018 -0.961 0.337
#> zPKC -0.015 0.017 -0.886 0.376
#> zRaf 0.736 0.019 37.861 0.000
#> zP38 ~
#> zPKA -0.000 0.019 -0.017 0.986
#> zPKC 0.652 0.018 35.760 0.000
#> zPIP2 ~
#> zPIP3 0.528 0.021 25.141 0.000
#> zPlcg 0.199 0.020 9.762 0.000
#> zPKC ~
#> zPIP2 0.029 0.025 1.163 0.245
#> zPlcg -0.010 0.026 -0.383 0.702
#> zPlcg ~
#> zPIP3 0.288 0.024 12.208 0.000
#> zRaf ~
#> zPKA 0.008 0.022 0.365 0.715
#> zPKC 0.007 0.021 0.348 0.728
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .zPIP3 ~~
#> .zPKA -0.016 0.022 -0.724 0.469
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .zAkt 0.671 0.023 29.715 0.000
#> .zErk 0.762 0.026 29.715 0.000
#> .zJnk 0.872 0.029 29.715 0.000
#> .zMek 0.523 0.018 29.715 0.000
#> .zP38 0.579 0.019 29.715 0.000
#> .zPIP2 0.653 0.022 29.715 0.000
#> .zPIP3 0.909 0.031 29.715 0.000
#> .zPKA 0.916 0.031 29.715 0.000
#> .zPKC 0.986 0.033 29.715 0.000
#> .zPlcg 0.891 0.030 29.715 0.000
#> .zRaf 0.785 0.026 29.715 0.000
#>
print(sem1$gest)
#> lhs op rhs est se z pvalue ci.lower ci.upper
#> 1 Akt ~ group 0.150 0.021 7.057 0.000 0.108 0.192
#> 2 Erk ~ group 0.179 0.022 8.046 0.000 0.135 0.222
#> 3 Jnk ~ group 0.333 0.023 14.279 0.000 0.288 0.379
#> 4 Mek ~ group 0.122 0.020 6.036 0.000 0.082 0.162
#> 5 P38 ~ group -0.062 0.019 -3.274 0.001 -0.100 -0.025
#> 6 PIP2 ~ group 0.110 0.021 5.243 0.000 0.069 0.150
#> 7 PIP3 ~ group -0.301 0.023 -13.278 0.000 -0.346 -0.257
#> 8 PKA ~ group 0.290 0.023 12.720 0.000 0.245 0.334
#> 9 PKC ~ group 0.116 0.024 4.818 0.000 0.069 0.163
#> 10 Plcg ~ group 0.268 0.024 11.359 0.000 0.222 0.314
#> 11 Raf ~ group -0.467 0.022 -21.080 0.000 -0.510 -0.423
head(parameterEstimates(sem1$fit))
#> lhs op rhs est se z pvalue ci.lower ci.upper
#> 1 Akt ~ group 0.150 0.021 7.057 0.000 0.108 0.192
#> 2 Erk ~ group 0.179 0.022 8.046 0.000 0.135 0.222
#> 3 Jnk ~ group 0.333 0.023 14.279 0.000 0.288 0.379
#> 4 Mek ~ group 0.122 0.020 6.036 0.000 0.082 0.162
#> 5 P38 ~ group -0.062 0.019 -3.274 0.001 -0.100 -0.025
#> 6 PIP2 ~ group 0.110 0.021 5.243 0.000 0.069 0.150
# Graphs
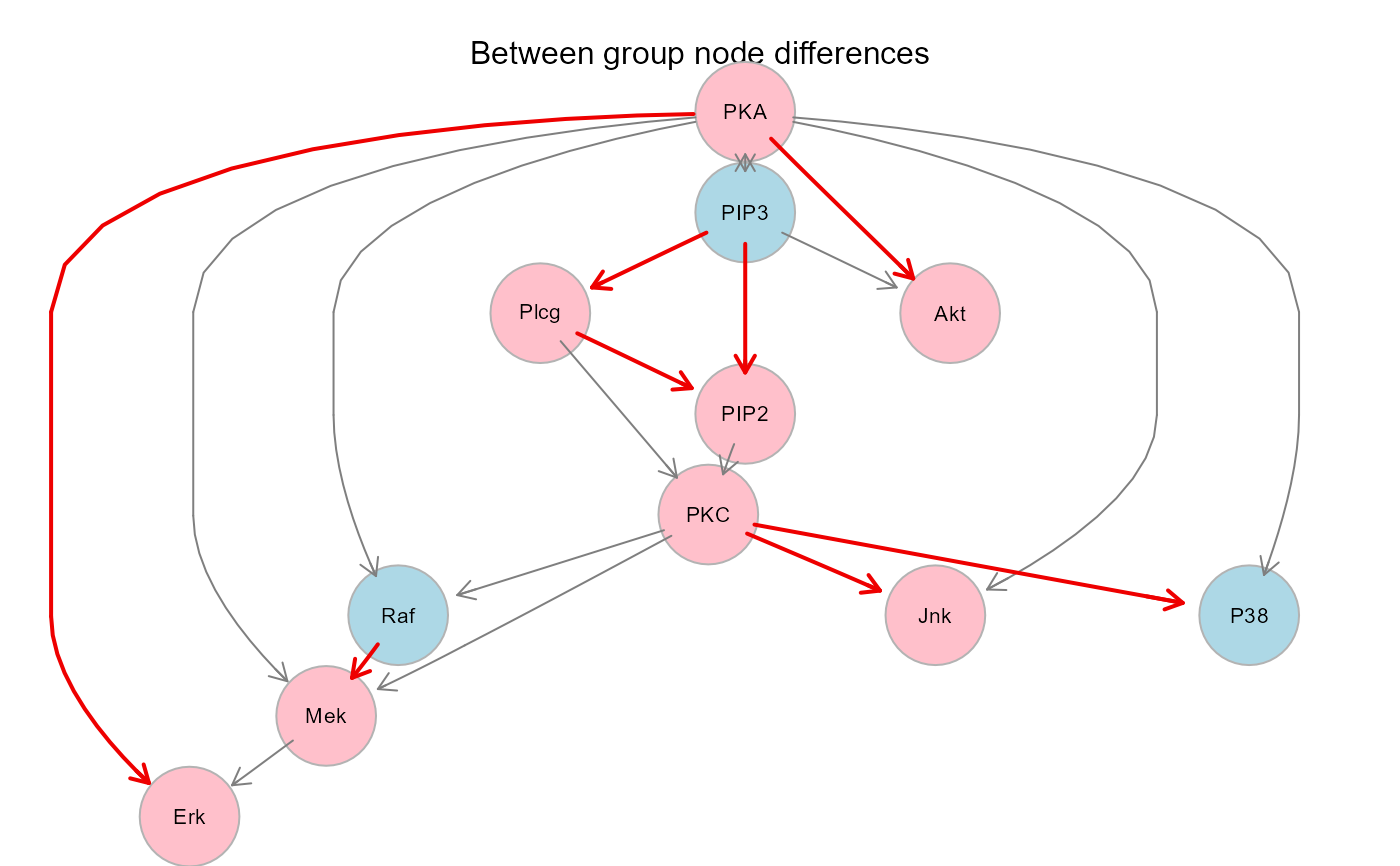
gplot(sem1$graph, main = "Between group node differences")
#### Model fitting (common model, group effect on nodes)
sem1 <- SEMrun(graph = sachs$graph, data = log(sachs$pkc),
group = sachs$group)
#> NLMINB solver ended normally after 5 iterations
#>
#> deviance/df: 61.84444 srmr: 0.0701161
#>
#> Brown's combined P-value of node activation: 2.664535e-15
#>
#> Brown's combined P-value of node inhibition: 0.2368274
#>
# Fitting summaries
summary(sem1$fit)
#> lavaan 0.6-20 ended normally after 5 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 41
#>
#> Number of observations 1766
#>
#> Model Test User Model:
#>
#> Test statistic 2226.396
#> Degrees of freedom 36
#> P-value (Chi-square) 0.000
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> zAkt ~
#> group 0.150 0.021 7.057 0.000
#> zErk ~
#> group 0.179 0.022 8.046 0.000
#> zJnk ~
#> group 0.333 0.023 14.279 0.000
#> zMek ~
#> group 0.122 0.020 6.036 0.000
#> zP38 ~
#> group -0.062 0.019 -3.274 0.001
#> zPIP2 ~
#> group 0.110 0.021 5.243 0.000
#> zPIP3 ~
#> group -0.301 0.023 -13.278 0.000
#> zPKA ~
#> group 0.290 0.023 12.720 0.000
#> zPKC ~
#> group 0.116 0.024 4.818 0.000
#> zPlcg ~
#> group 0.268 0.024 11.359 0.000
#> zRaf ~
#> group -0.467 0.022 -21.080 0.000
#> zAkt ~
#> zPIP3 -0.023 0.020 -1.148 0.251
#> zPKA 0.507 0.020 24.859 0.000
#> zErk ~
#> zMek 0.016 0.021 0.748 0.454
#> zPKA 0.407 0.022 18.760 0.000
#> zJnk ~
#> zPKA -0.002 0.023 -0.080 0.936
#> zPKC 0.096 0.022 4.284 0.000
#> zMek ~
#> zPKA -0.017 0.018 -0.961 0.337
#> zPKC -0.015 0.017 -0.886 0.376
#> zRaf 0.736 0.019 37.861 0.000
#> zP38 ~
#> zPKA -0.000 0.019 -0.017 0.986
#> zPKC 0.652 0.018 35.760 0.000
#> zPIP2 ~
#> zPIP3 0.528 0.021 25.141 0.000
#> zPlcg 0.199 0.020 9.762 0.000
#> zPKC ~
#> zPIP2 0.029 0.025 1.163 0.245
#> zPlcg -0.010 0.026 -0.383 0.702
#> zPlcg ~
#> zPIP3 0.288 0.024 12.208 0.000
#> zRaf ~
#> zPKA 0.008 0.022 0.365 0.715
#> zPKC 0.007 0.021 0.348 0.728
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> .zPIP3 ~~
#> .zPKA -0.016 0.022 -0.724 0.469
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .zAkt 0.671 0.023 29.715 0.000
#> .zErk 0.762 0.026 29.715 0.000
#> .zJnk 0.872 0.029 29.715 0.000
#> .zMek 0.523 0.018 29.715 0.000
#> .zP38 0.579 0.019 29.715 0.000
#> .zPIP2 0.653 0.022 29.715 0.000
#> .zPIP3 0.909 0.031 29.715 0.000
#> .zPKA 0.916 0.031 29.715 0.000
#> .zPKC 0.986 0.033 29.715 0.000
#> .zPlcg 0.891 0.030 29.715 0.000
#> .zRaf 0.785 0.026 29.715 0.000
#>
print(sem1$gest)
#> lhs op rhs est se z pvalue ci.lower ci.upper
#> 1 Akt ~ group 0.150 0.021 7.057 0.000 0.108 0.192
#> 2 Erk ~ group 0.179 0.022 8.046 0.000 0.135 0.222
#> 3 Jnk ~ group 0.333 0.023 14.279 0.000 0.288 0.379
#> 4 Mek ~ group 0.122 0.020 6.036 0.000 0.082 0.162
#> 5 P38 ~ group -0.062 0.019 -3.274 0.001 -0.100 -0.025
#> 6 PIP2 ~ group 0.110 0.021 5.243 0.000 0.069 0.150
#> 7 PIP3 ~ group -0.301 0.023 -13.278 0.000 -0.346 -0.257
#> 8 PKA ~ group 0.290 0.023 12.720 0.000 0.245 0.334
#> 9 PKC ~ group 0.116 0.024 4.818 0.000 0.069 0.163
#> 10 Plcg ~ group 0.268 0.024 11.359 0.000 0.222 0.314
#> 11 Raf ~ group -0.467 0.022 -21.080 0.000 -0.510 -0.423
head(parameterEstimates(sem1$fit))
#> lhs op rhs est se z pvalue ci.lower ci.upper
#> 1 Akt ~ group 0.150 0.021 7.057 0.000 0.108 0.192
#> 2 Erk ~ group 0.179 0.022 8.046 0.000 0.135 0.222
#> 3 Jnk ~ group 0.333 0.023 14.279 0.000 0.288 0.379
#> 4 Mek ~ group 0.122 0.020 6.036 0.000 0.082 0.162
#> 5 P38 ~ group -0.062 0.019 -3.274 0.001 -0.100 -0.025
#> 6 PIP2 ~ group 0.110 0.021 5.243 0.000 0.069 0.150
# Graphs
gplot(sem1$graph, main = "Between group node differences")
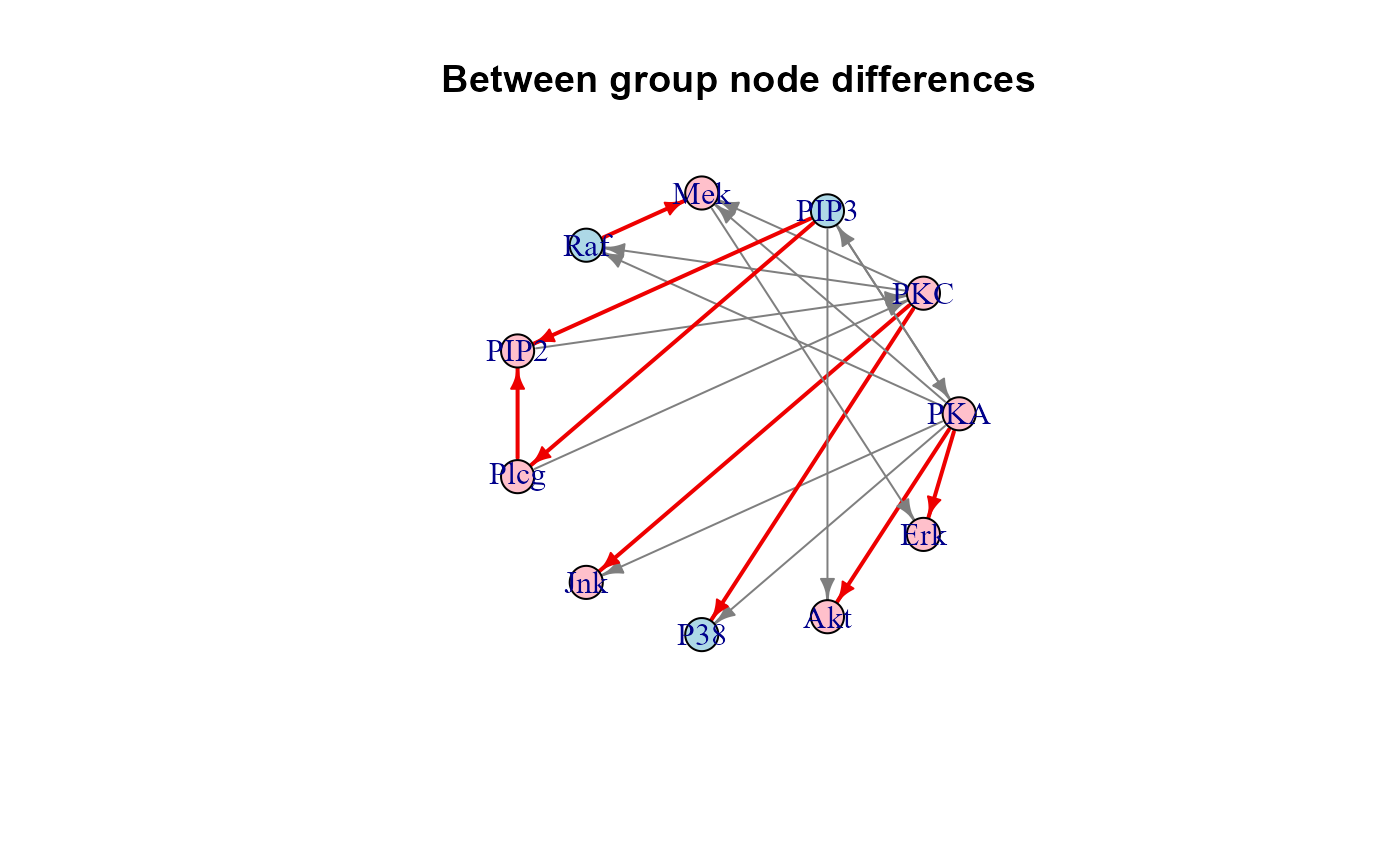
 plot(sem1$graph, layout = layout.circle, main = "Between group node differences")
plot(sem1$graph, layout = layout.circle, main = "Between group node differences")
 #### Two-group model fitting (group effect on edges)
sem2 <- SEMrun(graph = sachs$graph, data = log(sachs$pkc),
group = sachs$group,
fit = 2)
#> NLMINB solver ended normally after 12 iterations
#>
#> deviance/df: 31.19757 srmr: 0.0816294
#>
#> Brown's combined P-value of edge activation: 3.774758e-15
#>
#> Brown's combined P-value of edge inhibition: 0.9989142
#>
# Summaries
summary(sem2$fit)
#> lavaan 0.6-20 ended normally after 12 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 60
#>
#> Number of observations per group:
#> Group 1 853
#> Group 2 913
#>
#> Model Test User Model:
#>
#> Test statistic 2246.212
#> Degrees of freedom 72
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Group 1 877.592
#> Group 2 1368.621
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#>
#> Group 1 [Group 1]:
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> zAkt ~
#> zPIP3 -0.035 0.031 -1.129 0.259
#> zPKA 0.404 0.031 12.908 0.000
#> zErk ~
#> zMek 0.026 0.032 0.804 0.422
#> zPKA 0.351 0.032 10.936 0.000
#> zJnk ~
#> zPKA -0.003 0.034 -0.091 0.927
#> zPKC -0.202 0.034 -6.021 0.000
#> zMek ~
#> zPKA -0.002 0.025 -0.081 0.936
#> zPKC -0.019 0.025 -0.756 0.450
#> zRaf 0.678 0.025 26.971 0.000
#> zP38 ~
#> zPKA 0.008 0.028 0.286 0.775
#> zPKC 0.581 0.028 20.850 0.000
#> zPIP2 ~
#> zPIP3 0.350 0.032 10.854 0.000
#> zPlcg 0.003 0.032 0.092 0.927
#> zPKC ~
#> zPIP2 -0.017 0.034 -0.511 0.610
#> zPlcg -0.016 0.034 -0.455 0.649
#> zPlcg ~
#> zPIP3 0.090 0.034 2.653 0.008
#> zRaf ~
#> zPKA -0.003 0.034 -0.097 0.923
#> zPKC -0.033 0.034 -0.977 0.329
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> zPIP3 ~~
#> zPKA 0.011 0.034 0.315 0.753
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .zAkt 0.835 0.040 20.652 0.000
#> .zErk 0.876 0.042 20.652 0.000
#> .zJnk 0.958 0.046 20.652 0.000
#> .zMek 0.538 0.026 20.652 0.000
#> .zP38 0.661 0.032 20.652 0.000
#> .zPIP2 0.877 0.042 20.652 0.000
#> .zPKC 0.998 0.048 20.652 0.000
#> .zPlcg 0.991 0.048 20.652 0.000
#> .zRaf 0.998 0.048 20.652 0.000
#> zPIP3 0.999 0.048 20.652 0.000
#> zPKA 0.999 0.048 20.652 0.000
#>
#>
#> Group 2 [Group 2]:
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> zAkt ~
#> zPIP3 -0.007 0.026 -0.271 0.786
#> zPKA 0.616 0.026 23.631 0.000
#> zErk ~
#> zMek 0.011 0.029 0.391 0.696
#> zPKA 0.469 0.029 16.021 0.000
#> zJnk ~
#> zPKA 0.020 0.028 0.713 0.476
#> zPKC 0.523 0.028 18.558 0.000
#> zMek ~
#> zPKA -0.032 0.025 -1.278 0.201
#> zPKC -0.016 0.025 -0.634 0.526
#> zRaf 0.665 0.025 26.816 0.000
#> zP38 ~
#> zPKA 0.001 0.023 0.027 0.978
#> zPKC 0.718 0.023 31.170 0.000
#> zPIP2 ~
#> zPIP3 0.545 0.024 22.517 0.000
#> zPlcg 0.332 0.024 13.691 0.000
#> zPKC ~
#> zPIP2 0.078 0.040 1.963 0.050
#> zPlcg -0.027 0.040 -0.683 0.495
#> zPlcg ~
#> zPIP3 0.424 0.030 14.145 0.000
#> zRaf ~
#> zPKA 0.023 0.033 0.694 0.488
#> zPKC 0.049 0.033 1.493 0.136
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> zPIP3 ~~
#> zPKA -0.042 0.033 -1.275 0.202
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .zAkt 0.619 0.029 21.366 0.000
#> .zErk 0.780 0.036 21.366 0.000
#> .zJnk 0.725 0.034 21.366 0.000
#> .zMek 0.558 0.026 21.366 0.000
#> .zP38 0.484 0.023 21.366 0.000
#> .zPIP2 0.439 0.021 21.366 0.000
#> .zPKC 0.994 0.047 21.366 0.000
#> .zPlcg 0.819 0.038 21.366 0.000
#> .zRaf 0.996 0.047 21.366 0.000
#> zPIP3 0.999 0.047 21.366 0.000
#> zPKA 0.999 0.047 21.366 0.000
#>
print(sem2$dest)
#> lhs op rhs d_est d_se d_z pvalue d_lower d_upper
#> 1 Akt ~ PIP3 0.028 0.041 0.693 0.488 -0.052 0.108
#> 2 Akt ~ PKA 0.212 0.041 5.208 0.000 0.132 0.292
#> 3 Erk ~ Mek -0.014 0.043 -0.330 0.741 -0.099 0.071
#> 4 Erk ~ PKA 0.118 0.043 2.718 0.007 0.033 0.203
#> 5 Jnk ~ PKA 0.023 0.044 0.528 0.598 -0.063 0.109
#> 6 Jnk ~ PKC 0.725 0.044 16.544 0.000 0.639 0.811
#> 7 Mek ~ PKA -0.030 0.035 -0.839 0.402 -0.099 0.040
#> 8 Mek ~ PKC 0.003 0.035 0.094 0.925 -0.066 0.073
#> 9 Mek ~ Raf -0.014 0.035 -0.386 0.699 -0.083 0.056
#> 10 P38 ~ PKA -0.007 0.036 -0.203 0.839 -0.078 0.064
#> 11 P38 ~ PKC 0.137 0.036 3.777 0.000 0.066 0.208
#> 12 PIP2 ~ PIP3 0.196 0.040 4.858 0.000 0.117 0.275
#> 13 PIP2 ~ Plcg 0.329 0.040 8.155 0.000 0.250 0.408
#> 14 PKC ~ PIP2 0.096 0.053 1.823 0.068 -0.007 0.199
#> 15 PKC ~ Plcg -0.012 0.053 -0.223 0.824 -0.115 0.091
#> 16 Plcg ~ PIP3 0.334 0.045 7.346 0.000 0.245 0.422
#> 17 Raf ~ PKA 0.026 0.048 0.551 0.581 -0.067 0.120
#> 18 Raf ~ PKC 0.083 0.048 1.739 0.082 -0.011 0.176
head(parameterEstimates(sem2$fit))
#> lhs op rhs est se z pvalue ci.lower ci.upper group
#> 1 Akt ~ PIP3 -0.035 0.031 -1.129 0.259 -0.097 0.026 1
#> 2 Akt ~ PKA 0.404 0.031 12.908 0.000 0.343 0.465 1
#> 3 Erk ~ Mek 0.026 0.032 0.804 0.422 -0.037 0.089 1
#> 4 Erk ~ PKA 0.351 0.032 10.936 0.000 0.288 0.413 1
#> 5 Jnk ~ PKA -0.003 0.034 -0.091 0.927 -0.069 0.063 1
#> 6 Jnk ~ PKC -0.202 0.034 -6.021 0.000 -0.268 -0.136 1
# Graphs
gplot(sem2$graph, main = "Between group edge differences")
#### Two-group model fitting (group effect on edges)
sem2 <- SEMrun(graph = sachs$graph, data = log(sachs$pkc),
group = sachs$group,
fit = 2)
#> NLMINB solver ended normally after 12 iterations
#>
#> deviance/df: 31.19757 srmr: 0.0816294
#>
#> Brown's combined P-value of edge activation: 3.774758e-15
#>
#> Brown's combined P-value of edge inhibition: 0.9989142
#>
# Summaries
summary(sem2$fit)
#> lavaan 0.6-20 ended normally after 12 iterations
#>
#> Estimator ML
#> Optimization method NLMINB
#> Number of model parameters 60
#>
#> Number of observations per group:
#> Group 1 853
#> Group 2 913
#>
#> Model Test User Model:
#>
#> Test statistic 2246.212
#> Degrees of freedom 72
#> P-value (Chi-square) 0.000
#> Test statistic for each group:
#> Group 1 877.592
#> Group 2 1368.621
#>
#> Parameter Estimates:
#>
#> Standard errors Standard
#> Information Observed
#> Observed information based on Hessian
#>
#>
#> Group 1 [Group 1]:
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> zAkt ~
#> zPIP3 -0.035 0.031 -1.129 0.259
#> zPKA 0.404 0.031 12.908 0.000
#> zErk ~
#> zMek 0.026 0.032 0.804 0.422
#> zPKA 0.351 0.032 10.936 0.000
#> zJnk ~
#> zPKA -0.003 0.034 -0.091 0.927
#> zPKC -0.202 0.034 -6.021 0.000
#> zMek ~
#> zPKA -0.002 0.025 -0.081 0.936
#> zPKC -0.019 0.025 -0.756 0.450
#> zRaf 0.678 0.025 26.971 0.000
#> zP38 ~
#> zPKA 0.008 0.028 0.286 0.775
#> zPKC 0.581 0.028 20.850 0.000
#> zPIP2 ~
#> zPIP3 0.350 0.032 10.854 0.000
#> zPlcg 0.003 0.032 0.092 0.927
#> zPKC ~
#> zPIP2 -0.017 0.034 -0.511 0.610
#> zPlcg -0.016 0.034 -0.455 0.649
#> zPlcg ~
#> zPIP3 0.090 0.034 2.653 0.008
#> zRaf ~
#> zPKA -0.003 0.034 -0.097 0.923
#> zPKC -0.033 0.034 -0.977 0.329
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> zPIP3 ~~
#> zPKA 0.011 0.034 0.315 0.753
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .zAkt 0.835 0.040 20.652 0.000
#> .zErk 0.876 0.042 20.652 0.000
#> .zJnk 0.958 0.046 20.652 0.000
#> .zMek 0.538 0.026 20.652 0.000
#> .zP38 0.661 0.032 20.652 0.000
#> .zPIP2 0.877 0.042 20.652 0.000
#> .zPKC 0.998 0.048 20.652 0.000
#> .zPlcg 0.991 0.048 20.652 0.000
#> .zRaf 0.998 0.048 20.652 0.000
#> zPIP3 0.999 0.048 20.652 0.000
#> zPKA 0.999 0.048 20.652 0.000
#>
#>
#> Group 2 [Group 2]:
#>
#> Regressions:
#> Estimate Std.Err z-value P(>|z|)
#> zAkt ~
#> zPIP3 -0.007 0.026 -0.271 0.786
#> zPKA 0.616 0.026 23.631 0.000
#> zErk ~
#> zMek 0.011 0.029 0.391 0.696
#> zPKA 0.469 0.029 16.021 0.000
#> zJnk ~
#> zPKA 0.020 0.028 0.713 0.476
#> zPKC 0.523 0.028 18.558 0.000
#> zMek ~
#> zPKA -0.032 0.025 -1.278 0.201
#> zPKC -0.016 0.025 -0.634 0.526
#> zRaf 0.665 0.025 26.816 0.000
#> zP38 ~
#> zPKA 0.001 0.023 0.027 0.978
#> zPKC 0.718 0.023 31.170 0.000
#> zPIP2 ~
#> zPIP3 0.545 0.024 22.517 0.000
#> zPlcg 0.332 0.024 13.691 0.000
#> zPKC ~
#> zPIP2 0.078 0.040 1.963 0.050
#> zPlcg -0.027 0.040 -0.683 0.495
#> zPlcg ~
#> zPIP3 0.424 0.030 14.145 0.000
#> zRaf ~
#> zPKA 0.023 0.033 0.694 0.488
#> zPKC 0.049 0.033 1.493 0.136
#>
#> Covariances:
#> Estimate Std.Err z-value P(>|z|)
#> zPIP3 ~~
#> zPKA -0.042 0.033 -1.275 0.202
#>
#> Variances:
#> Estimate Std.Err z-value P(>|z|)
#> .zAkt 0.619 0.029 21.366 0.000
#> .zErk 0.780 0.036 21.366 0.000
#> .zJnk 0.725 0.034 21.366 0.000
#> .zMek 0.558 0.026 21.366 0.000
#> .zP38 0.484 0.023 21.366 0.000
#> .zPIP2 0.439 0.021 21.366 0.000
#> .zPKC 0.994 0.047 21.366 0.000
#> .zPlcg 0.819 0.038 21.366 0.000
#> .zRaf 0.996 0.047 21.366 0.000
#> zPIP3 0.999 0.047 21.366 0.000
#> zPKA 0.999 0.047 21.366 0.000
#>
print(sem2$dest)
#> lhs op rhs d_est d_se d_z pvalue d_lower d_upper
#> 1 Akt ~ PIP3 0.028 0.041 0.693 0.488 -0.052 0.108
#> 2 Akt ~ PKA 0.212 0.041 5.208 0.000 0.132 0.292
#> 3 Erk ~ Mek -0.014 0.043 -0.330 0.741 -0.099 0.071
#> 4 Erk ~ PKA 0.118 0.043 2.718 0.007 0.033 0.203
#> 5 Jnk ~ PKA 0.023 0.044 0.528 0.598 -0.063 0.109
#> 6 Jnk ~ PKC 0.725 0.044 16.544 0.000 0.639 0.811
#> 7 Mek ~ PKA -0.030 0.035 -0.839 0.402 -0.099 0.040
#> 8 Mek ~ PKC 0.003 0.035 0.094 0.925 -0.066 0.073
#> 9 Mek ~ Raf -0.014 0.035 -0.386 0.699 -0.083 0.056
#> 10 P38 ~ PKA -0.007 0.036 -0.203 0.839 -0.078 0.064
#> 11 P38 ~ PKC 0.137 0.036 3.777 0.000 0.066 0.208
#> 12 PIP2 ~ PIP3 0.196 0.040 4.858 0.000 0.117 0.275
#> 13 PIP2 ~ Plcg 0.329 0.040 8.155 0.000 0.250 0.408
#> 14 PKC ~ PIP2 0.096 0.053 1.823 0.068 -0.007 0.199
#> 15 PKC ~ Plcg -0.012 0.053 -0.223 0.824 -0.115 0.091
#> 16 Plcg ~ PIP3 0.334 0.045 7.346 0.000 0.245 0.422
#> 17 Raf ~ PKA 0.026 0.048 0.551 0.581 -0.067 0.120
#> 18 Raf ~ PKC 0.083 0.048 1.739 0.082 -0.011 0.176
head(parameterEstimates(sem2$fit))
#> lhs op rhs est se z pvalue ci.lower ci.upper group
#> 1 Akt ~ PIP3 -0.035 0.031 -1.129 0.259 -0.097 0.026 1
#> 2 Akt ~ PKA 0.404 0.031 12.908 0.000 0.343 0.465 1
#> 3 Erk ~ Mek 0.026 0.032 0.804 0.422 -0.037 0.089 1
#> 4 Erk ~ PKA 0.351 0.032 10.936 0.000 0.288 0.413 1
#> 5 Jnk ~ PKA -0.003 0.034 -0.091 0.927 -0.069 0.063 1
#> 6 Jnk ~ PKC -0.202 0.034 -6.021 0.000 -0.268 -0.136 1
# Graphs
gplot(sem2$graph, main = "Between group edge differences")
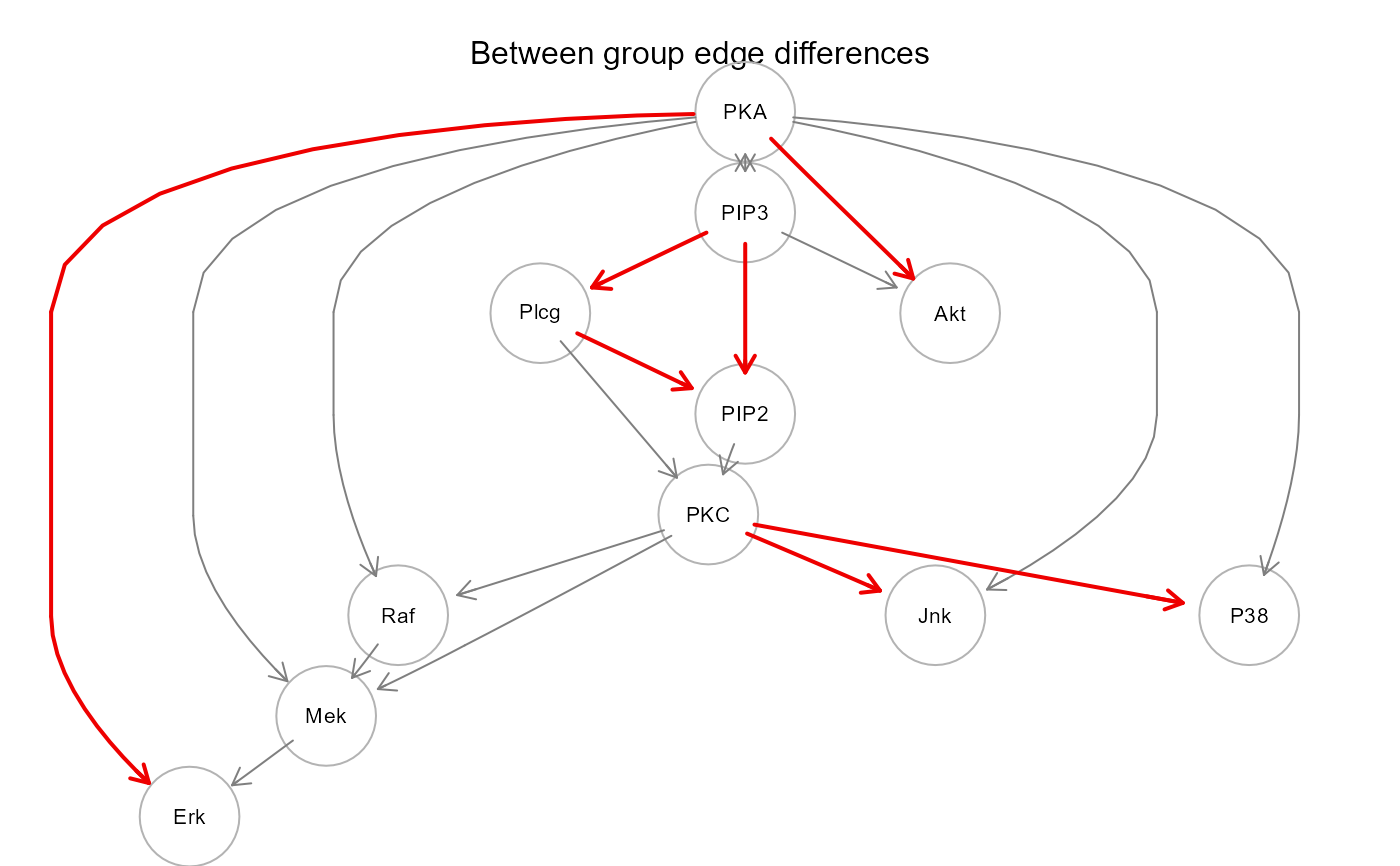 plot(sem2$graph, layout = layout.circle, main = "Between group edge differences")
plot(sem2$graph, layout = layout.circle, main = "Between group edge differences")
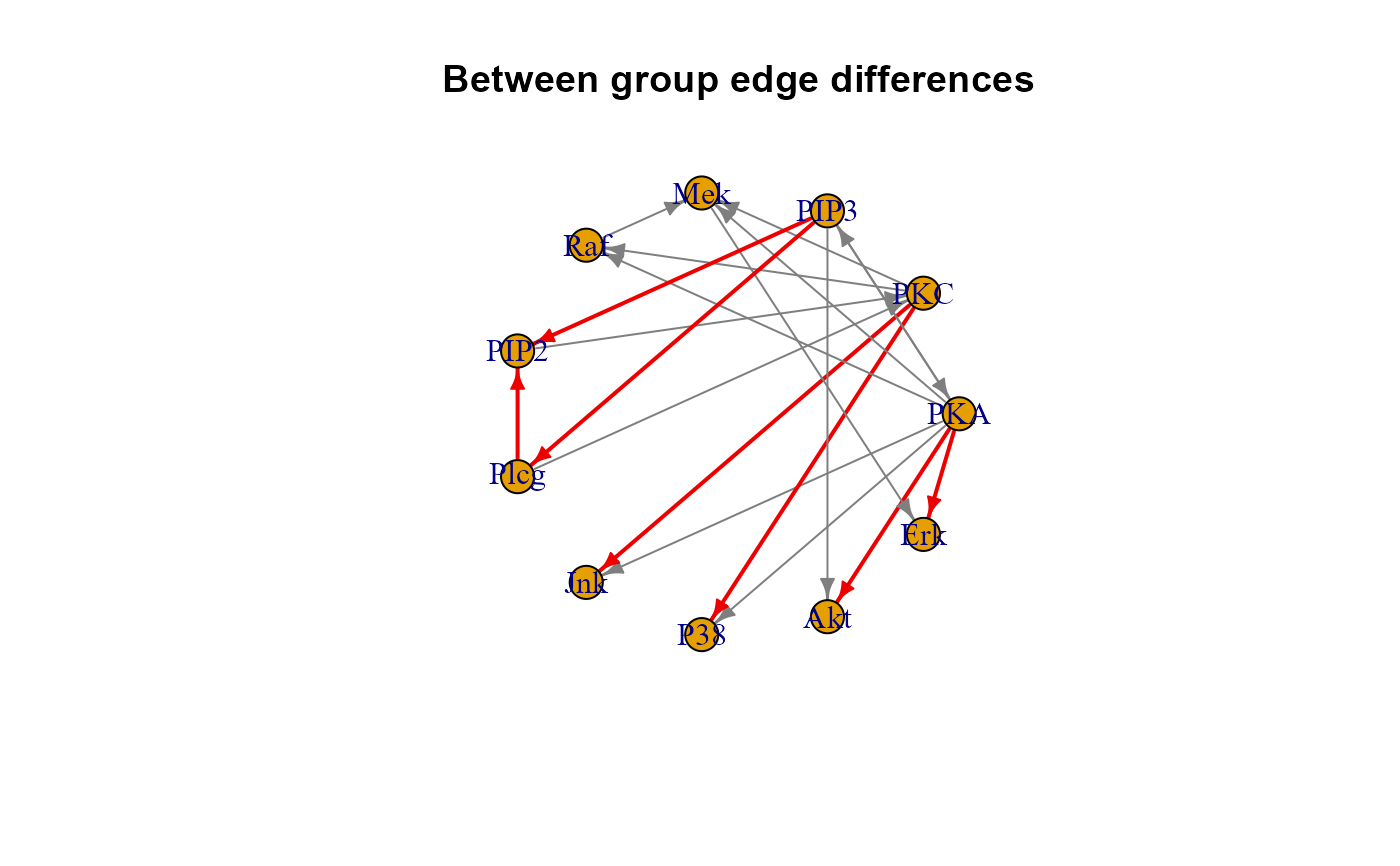 # \donttest{
# Fitting and visualization of a large pathway:
g <- kegg.pathways[["Neurotrophin signaling pathway"]]
G <- properties(g)[[1]]
#> Frequency distribution of graph components
#>
#> n.nodes n.graphs
#> 1 117 1
#>
#> Percent of vertices in the giant component: 98.3 %
#>
#> is.simple is.dag is.directed is.weighted
#> TRUE FALSE TRUE TRUE
#>
#> which.mutual.FALSE
#> 357
summary(G)
#> IGRAPH 7c83223 DNW- 117 357 --
#> + attr: name (v/c), weight (e/n)
# Nonparanormal(npn) transformation
als.npn <- transformData(alsData$exprs)$data
#> Conducting the nonparanormal transformation via shrunkun ECDF...done.
g1 <- SEMrun(G, als.npn, alsData$group, algo = "cggm")$graph
#> DAG conversion : TRUE
#> GGM (de-biased nodewise L1) solver ended normally after 108 iterations
#>
#> deviance/df: 5.620736 srmr: 0.3141688
#>
#> Brown's combined P-value of node activation: 1.110223e-14
#>
#> Brown's combined P-value of node inhibition: 7.771561e-16
#>
g2 <- SEMrun(g1, als.npn, alsData$group, fit = 2, algo = "cggm")$graph
#> GGM (de-biased nodewise L1) solver ended normally after 0 iterations
#>
#> deviance/df: 8.78412 srmr: 0.3490261
#>
#> Brown's combined P-value of edge activation: 8.634204e-13
#>
#> Brown's combined P-value of edge inhibition: 6.747936e-13
#>
# extract the subgraph with node and edge differences
g2 <- g2 - E(g2)[-which(E(g2)$color != "gray50")]
g <- properties(g2)[[1]]
#> Frequency distribution of graph components
#>
#> n.nodes n.graphs
#> 1 2 5
#> 2 3 2
#> 3 6 1
#> 4 9 1
#> 5 32 1
#>
#> Percent of vertices in the giant component: 29.6 %
#>
#> is.simple is.dag is.directed is.weighted
#> TRUE TRUE TRUE TRUE
#>
#> which.mutual.FALSE
#> 35
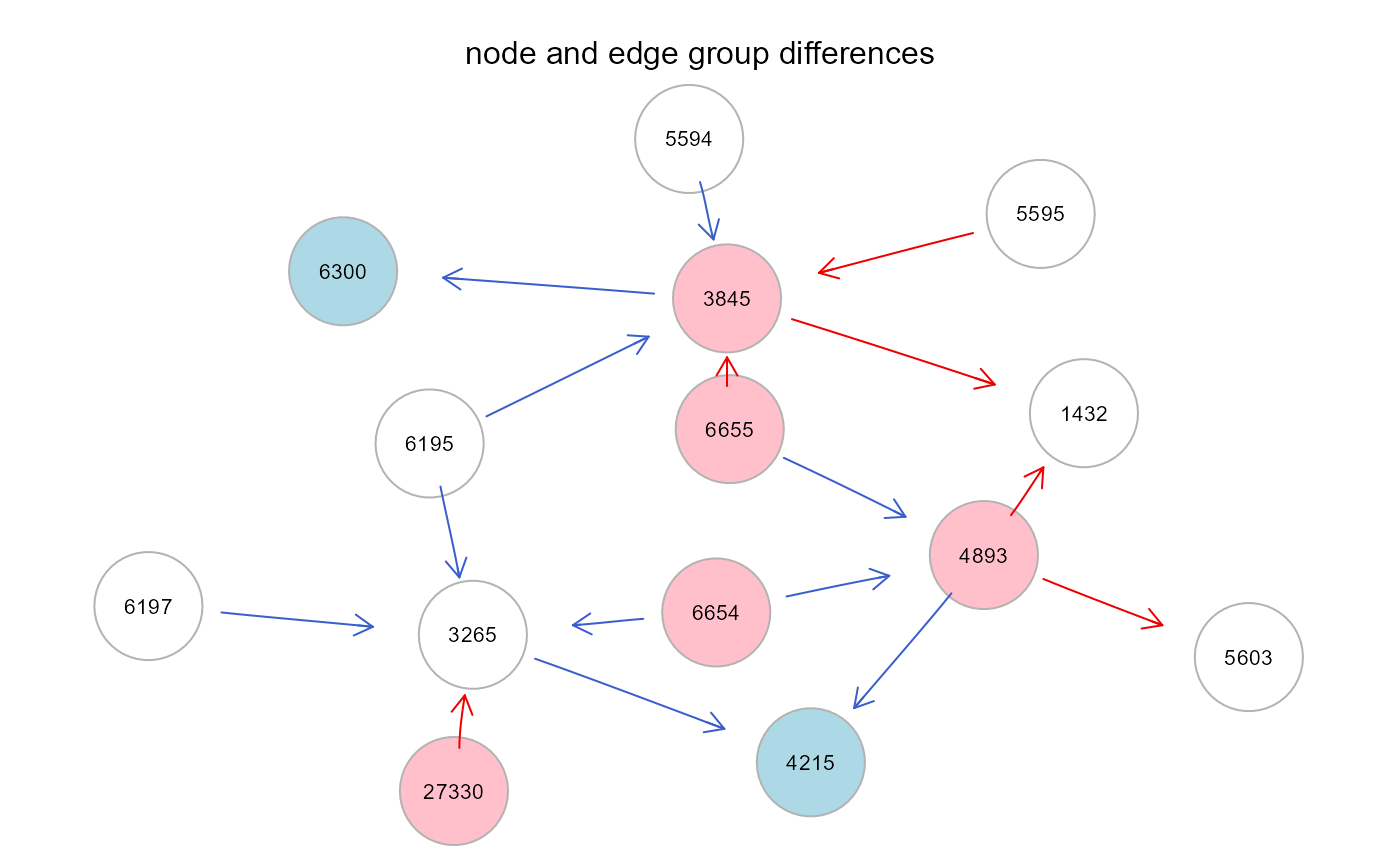
# plot graph
E(g)$color<- E(g2)$color[E(g2) %in% E(g)]
gplot(g, l="fdp", psize=40, main="node and edge group differences")
# \donttest{
# Fitting and visualization of a large pathway:
g <- kegg.pathways[["Neurotrophin signaling pathway"]]
G <- properties(g)[[1]]
#> Frequency distribution of graph components
#>
#> n.nodes n.graphs
#> 1 117 1
#>
#> Percent of vertices in the giant component: 98.3 %
#>
#> is.simple is.dag is.directed is.weighted
#> TRUE FALSE TRUE TRUE
#>
#> which.mutual.FALSE
#> 357
summary(G)
#> IGRAPH 7c83223 DNW- 117 357 --
#> + attr: name (v/c), weight (e/n)
# Nonparanormal(npn) transformation
als.npn <- transformData(alsData$exprs)$data
#> Conducting the nonparanormal transformation via shrunkun ECDF...done.
g1 <- SEMrun(G, als.npn, alsData$group, algo = "cggm")$graph
#> DAG conversion : TRUE
#> GGM (de-biased nodewise L1) solver ended normally after 108 iterations
#>
#> deviance/df: 5.620736 srmr: 0.3141688
#>
#> Brown's combined P-value of node activation: 1.110223e-14
#>
#> Brown's combined P-value of node inhibition: 7.771561e-16
#>
g2 <- SEMrun(g1, als.npn, alsData$group, fit = 2, algo = "cggm")$graph
#> GGM (de-biased nodewise L1) solver ended normally after 0 iterations
#>
#> deviance/df: 8.78412 srmr: 0.3490261
#>
#> Brown's combined P-value of edge activation: 8.634204e-13
#>
#> Brown's combined P-value of edge inhibition: 6.747936e-13
#>
# extract the subgraph with node and edge differences
g2 <- g2 - E(g2)[-which(E(g2)$color != "gray50")]
g <- properties(g2)[[1]]
#> Frequency distribution of graph components
#>
#> n.nodes n.graphs
#> 1 2 5
#> 2 3 2
#> 3 6 1
#> 4 9 1
#> 5 32 1
#>
#> Percent of vertices in the giant component: 29.6 %
#>
#> is.simple is.dag is.directed is.weighted
#> TRUE TRUE TRUE TRUE
#>
#> which.mutual.FALSE
#> 35
# plot graph
E(g)$color<- E(g2)$color[E(g2) %in% E(g)]
gplot(g, l="fdp", psize=40, main="node and edge group differences")
 # }
# }