SEM-based out-of-sample predictions

Source: R/semTools.R

Given the values of (observed) x-variables in a structural equation model, this function may be used to predict the values of (observed) y-variables. Response variables (y) represent sink nodes, and predictor variables (x) might consist of either (i) just source nodes or (ii) source and mediators from the fitted graph structure.

predictSink(
  object,
  newdata = NULL,
  K_fold = 5,
  source = FALSE,
  verbose = FALSE,
  ...
)

Arguments

object

An object, as that created by the function SEMrun() with the argument fit set to fit = 0 or fit = 1.

newdata

An optional matrix with rows corresponding to subjects, and columns to graph nodes (variables). If object$fit is a model with the group variable (fit = 1), the first column of newdata must be the new group binary vector (0=control, 1=case). As a default newdata = NULL, meaning that the K-fold cross validation is applied on the object$data. Conversely, if the argument newdata is specified, this matrix will be used for testing (out-of-sample predictions) and object$data will be used for training.

K_fold

The number of subsets (folds) into which the data will be partitioned for performing K-fold cross-validation. The model is refit K times, each time leaving out one of the K folds (default, K_fold=5). If the argument newdata is specified, the K-fold cross validation will not be done.

source

A logical value. If FALSE (default), the predictor variables (x) include source and mediators. If TRUE, x includes only the source nodes.

verbose

A logical value. If FALSE (default), the processed graph will not be plotted to screen.

...

Currently ignored.

Value

A list of 3 objects:

  1. "yobs", the matrix of observed continuous values of sink nodes based on out-of-bag samples.

  2. "yhat", the matrix of continuous predicted values of sink nodes ased on out-of-bag samples.

  3. "PE", vector of the prediction error equal to the Root Mean Squared Error (RMSE) for each out-of-bag sink prediction. The first value of PE is the total RMSE, where we sum over all sink nodes.

Details

The function uses a SEM-based predictive approach (Rooij et al., 2022) to produce predictions while accounting for the given graph structure. Predictions (for y given x) are based on the (joint y and x) model-implied variance-covariance (Sigma) matrix and mean vector (Mu) of the fitted SEM, and the standard expression for the conditional mean of a multivariate normal distribution. Thus, the structure described in the SEM is taken into consideration, which differs from ordinary least squares (OLS) regression. Note that if the model is saturated (and hence df = 0), or when source = TRUE, i.e., the set of predictors will include only the source nodes, the SEM-based predictions are identical or similar to OLS predictions.

References

de Rooij M, Karch JD, Fokkema M, Bakk Z, Pratiwi BC, and Kelderman H (2023). SEM-Based Out-of-Sample Predictions, Structural Equation Modeling: A Multidisciplinary Journal, 30:1, 132-148 <https://doi.org/10.1080/10705511.2022.2061494>

Author

Mario Grassi mario.grassi@unipv.it

Examples


# load ALS data
ig<- alsData$graph
X<- alsData$exprs
X<- transformData(X)$data
#> Conducting the nonparanormal transformation via shrunkun ECDF...done.
group<- alsData$group

#...with train-test (0.8-0.2) samples
set.seed(1)
train<- sample(1:nrow(X), 0.8*nrow(X))

# SEM fitting
#sem0<- SEMrun(ig, X[train,], algo="lavaan", SE="none")
#sem0<- SEMrun(ig, X[train,], algo="ricf", n_rep=0)
sem0<- SEMrun(ig, X[train,], algo="cggm")
#> GGM (de-biased nodewise L1) solver ended normally after 23 iterations 
#> 
#> deviance/df: 9.106766  srmr: 0.2894355 
#> 

# predictors, source+mediator variables
res1<- predictSink(sem0, newdata=X[-train,]) 
print(res1$PE)
#>     RMSEp     10452     84134       836      4747      4741      4744     79139 
#> 0.8947749 1.0326231 1.0087524 0.8553774 0.7786587 0.8996807 0.9121191 0.8560693 
#>      5530      5532      5533      5534      5535 
#> 0.8894708 0.8057714 0.9877559 0.8883097 0.7785695 

# predictors, source variables
res2<- predictSink(sem0, newdata=X[-train,], source=TRUE) 
print(res2$PE)
#>     RMSEp     10452     84134       836      4747      4741      4744     79139 
#> 0.9233759 1.0326231 1.0087524 0.9275277 0.9182175 0.9723922 0.9769343 0.8560693 
#>      5530      5532      5533      5534      5535 
#> 0.8894708 0.8057714 0.9877559 0.8883097 0.7785695 

#...with 5-fold cross-validation samples
set.seed(2)

# SEM fitting
#sem0<- SEMrun(ig, X, algo="lavaan", SE="none")
#sem0<- SEMrun(ig, X, algo="ricf", n_rep=0)
sem0<- SEMrun(ig, X, algo="cggm")
#> GGM (de-biased nodewise L1) solver ended normally after 23 iterations 
#> 
#> deviance/df: 10.92484  srmr: 0.2858581 
#> 

# predictors, source+mediator variables  
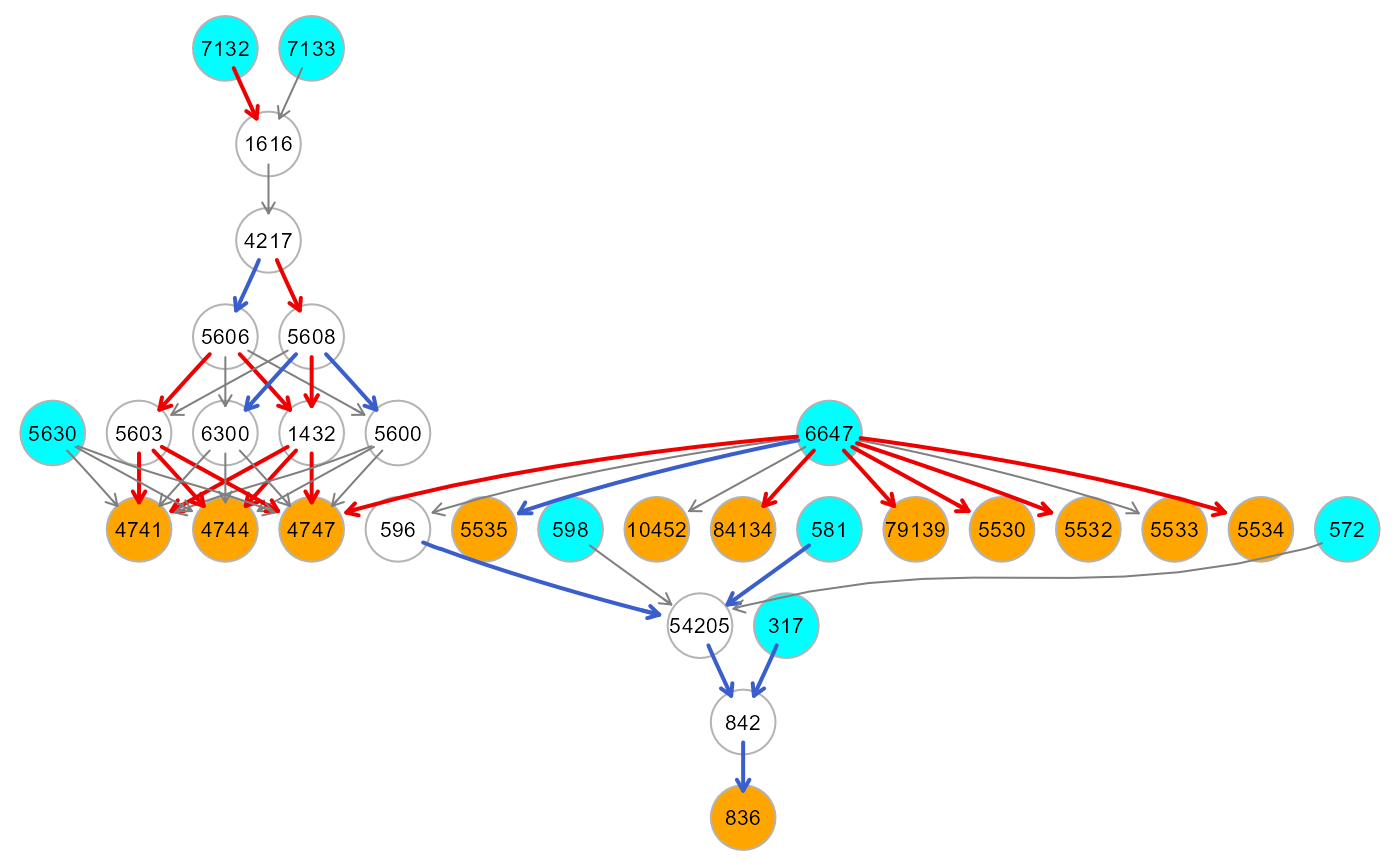
res3<- predictSink(sem0, K_fold = 5, verbose=TRUE)
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5

#>     RMSEp     10452     84134       836      4747      4741      4744     79139 
#> 0.9080455 0.9881723 0.9669898 0.8646300 0.7541061 0.9270740 0.9666216 0.8537759 
#>      5530      5532      5533      5534      5535 
#> 0.9191963 0.8624129 0.9852940 0.9016399 0.8783801 
print(res3$PE)
#>     RMSEp     10452     84134       836      4747      4741      4744     79139 
#> 0.9080455 0.9881723 0.9669898 0.8646300 0.7541061 0.9270740 0.9666216 0.8537759 
#>      5530      5532      5533      5534      5535 
#> 0.9191963 0.8624129 0.9852940 0.9016399 0.8783801 

# predictors, source variables
res4<- predictSink(sem0, K_fold = 5, source=TRUE, verbose=TRUE) 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5

#>     RMSEp     10452     84134       836      4747      4741      4744     79139 
#> 0.8082998 0.6998572 0.7681546 0.8084107 0.7953529 0.9582077 0.9821418 0.7670272 
#>      5530      5532      5533      5534      5535 
#> 0.7253268 0.7123354 0.9349106 0.7491959 0.7309169 
print(res4$PE)
#>     RMSEp     10452     84134       836      4747      4741      4744     79139 
#> 0.8082998 0.6998572 0.7681546 0.8084107 0.7953529 0.9582077 0.9821418 0.7670272 
#>      5530      5532      5533      5534      5535 
#> 0.7253268 0.7123354 0.9349106 0.7491959 0.7309169 

# \dontrun{

#...with 10-fold cross-validation samples and 10-iterations

# SEM fitting
#sem1<- SEMrun(ig, X, group, algo="lavaan", SE="none")
#sem1<- SEMrun(ig, X, group, algo="ricf", n_rep=0)
sem1<- SEMrun(ig, X, group, algo="cggm")
#> GGM (de-biased nodewise L1) solver ended normally after 31 iterations 
#> 
#> deviance/df: 11.02563  srmr: 0.2748964 
#> 
#> Brown's combined P-value of node activation: 7.626181e-08 
#> 
#> Brown's combined P-value of node inhibition: 0.01119587 
#> 

# predictors, source+mediator+group variables
res<- NULL
for (r in 1:10) {
  set.seed(r)
  cat("rep = ", r, "\n")
  resr<- predictSink(sem1, K_fold = 10)
  res<- rbind(res, resr$PE)
}
#> rep =  1 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  2 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  3 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  4 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  5 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  6 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  7 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  8 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  9 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
#> rep =  10 
#> Fold: 1
#> Fold: 2
#> Fold: 3
#> Fold: 4
#> Fold: 5
#> Fold: 6
#> Fold: 7
#> Fold: 8
#> Fold: 9
#> Fold: 10
res
#>           RMSEp     10452     84134       836      4747      4741      4744
#>  [1,] 0.9053291 0.9785624 0.9604402 0.8644252 0.7640509 0.9238181 0.9519654
#>  [2,] 0.9073665 0.9751398 0.9516419 0.8778027 0.7707494 0.9239893 0.9530069
#>  [3,] 0.8973367 0.9756381 0.9455834 0.8710680 0.7381597 0.9180007 0.9557306
#>  [4,] 0.9083096 0.9928931 0.9524679 0.8767483 0.7794402 0.9434862 0.9698471
#>  [5,] 0.8995353 0.9775423 0.9468809 0.8743403 0.7700005 0.9350917 0.9412939
#>  [6,] 0.9057364 0.9830704 0.9704686 0.8667298 0.7804901 0.9274886 0.9375883
#>  [7,] 0.8993322 0.9765749 0.9577832 0.8738061 0.7572529 0.9281862 0.9560545
#>  [8,] 0.9010274 0.9755777 0.9437476 0.8709026 0.7353162 0.9163567 0.9659085
#>  [9,] 0.9077804 0.9797885 0.9562588 0.8818664 0.7818231 0.9336874 0.9440139
#> [10,] 0.9025314 0.9723674 0.9561812 0.8902935 0.7643725 0.9259726 0.9350089
#>           79139      5530      5532      5533      5534      5535
#>  [1,] 0.8649838 0.9054969 0.8618371 0.9739843 0.9149784 0.8763687
#>  [2,] 0.8689036 0.9148508 0.8694880 0.9752280 0.9148275 0.8722064
#>  [3,] 0.8382332 0.8970001 0.8485723 0.9721229 0.9057523 0.8740974
#>  [4,] 0.8494831 0.8991107 0.8475546 0.9726572 0.8984859 0.8936386
#>  [5,] 0.8466404 0.8983633 0.8390027 0.9700215 0.8889163 0.8837956
#>  [6,] 0.8505063 0.9096460 0.8572574 0.9732127 0.9130431 0.8774249
#>  [7,] 0.8284438 0.8990238 0.8453252 0.9877291 0.8948298 0.8582123
#>  [8,] 0.8755581 0.9081759 0.8571685 0.9724900 0.9060706 0.8573912
#>  [9,] 0.8455938 0.9069533 0.8582371 0.9723112 0.9098083 0.9028805
#> [10,] 0.8471626 0.9054497 0.8593273 0.9776906 0.9050977 0.8691210
apply(res, 2, mean)
#>     RMSEp     10452     84134       836      4747      4741      4744     79139 
#> 0.9034285 0.9787155 0.9541454 0.8747983 0.7641656 0.9276077 0.9510418 0.8515509 
#>      5530      5532      5533      5534      5535 
#> 0.9044071 0.8543770 0.9747448 0.9051810 0.8765136 

# }