Vertex and edge graph coloring on the base of fitting

Add vertex and edge color attributes to an igraph object, based on a fitting results data.frame generated by SEMrun.

colorGraph(
  est,
  graph,
  group,
  method = "none",
  alpha = 0.05,
  vcolor = c("lightblue", "white", "pink"),
  ecolor = c("royalblue3", "gray50", "red2"),
  ewidth = c(1, 2),
  ...
)

Arguments

est: A data.frame of estimated parameters and p-values, derived from the fit object returned by SEMrun. As an alternative, the user may provide a "gest" or "dest" data.frame generated by SEMrun.
graph: An igraph object.
group: group A binary vector. This vector must be as long as the number of subjects. Each vector element must be 1 for cases and 0 for control subjects.
method: Multiple testing correction method. One of the values available in p.adjust. By default, method is set to "none" (i.e., no multiple test correction).
alpha: Significance level for node and edge coloring (by default, alpha = 0.05).
vcolor: A vector of three color names. The first color is given to nodes with P-value < alpha and beta < 0, the third color is given to nodes with P-value < alpha and beta > 0, and the second is given to nodes with P-value > alpha. By default, vcolor = c("lightblue", "white", "pink").
ecolor: A vector of three color names. The first color is given to edges with P-value < alpha and regression coefficient < 0, the third color is given to edges with P-value < alpha and regression coefficient > 0, and the second is given to edges with P-value > alpha. By default, vcolor = c("blue", "gray50", "red2").
ewidth: A vector of two values. The first value refers to the basic edge width (i.e., edges with P-value > alpha), while the second is given to edges with P-value < alpha. By default ewidth = c(1, 2).
...: Currently ignored.

Value

An igraph object with vertex and edge color and width attributes.

Author

Mario Grassi mario.grassi@unipv.it

Examples


# \donttest{

# Model fitting: node perturbation
sem1 <- SEMrun(graph = alsData$graph, data = alsData$exprs,
               group = alsData$group,
               fit = 1)
#> NLMINB solver ended normally after 1 iterations 
#> 
#> deviance/df: 12.66492  srmr: 0.303644 
#> 
#> Brown's combined P-value of node activation: 8.943957e-13 
#> 
#> Brown's combined P-value of node inhibition: 0.02173378 
#> 
est1 <- parameterEstimates(sem1$fit)

# Model fitting: edge perturbation
sem2 <- SEMrun(graph = alsData$graph, data = alsData$exprs,
               group = alsData$group,
               fit = 2)
#> Estimating optimal shrinkage intensity lambda (correlation matrix): 0.4547 
#> 
#> NLMINB solver ended normally after 7 iterations 
#> 
#> deviance/df: 16.74697  srmr: 0.3247998 
#> 
#> Brown's combined P-value of edge activation: 0.01363458 
#> 
#> Brown's combined P-value of edge inhibition: 0.8656962 
#> 
est20 <- subset(parameterEstimates(sem2$fit), group == 1)[, -c(4, 5)]
est21 <- subset(parameterEstimates(sem2$fit), group == 2)[, -c(4, 5)]

# Graphs
g <- alsData$graph
x <- alsData$group

old.par <- par(no.readonly = TRUE)
par(mfrow=c(2,2), mar=rep(1,4))
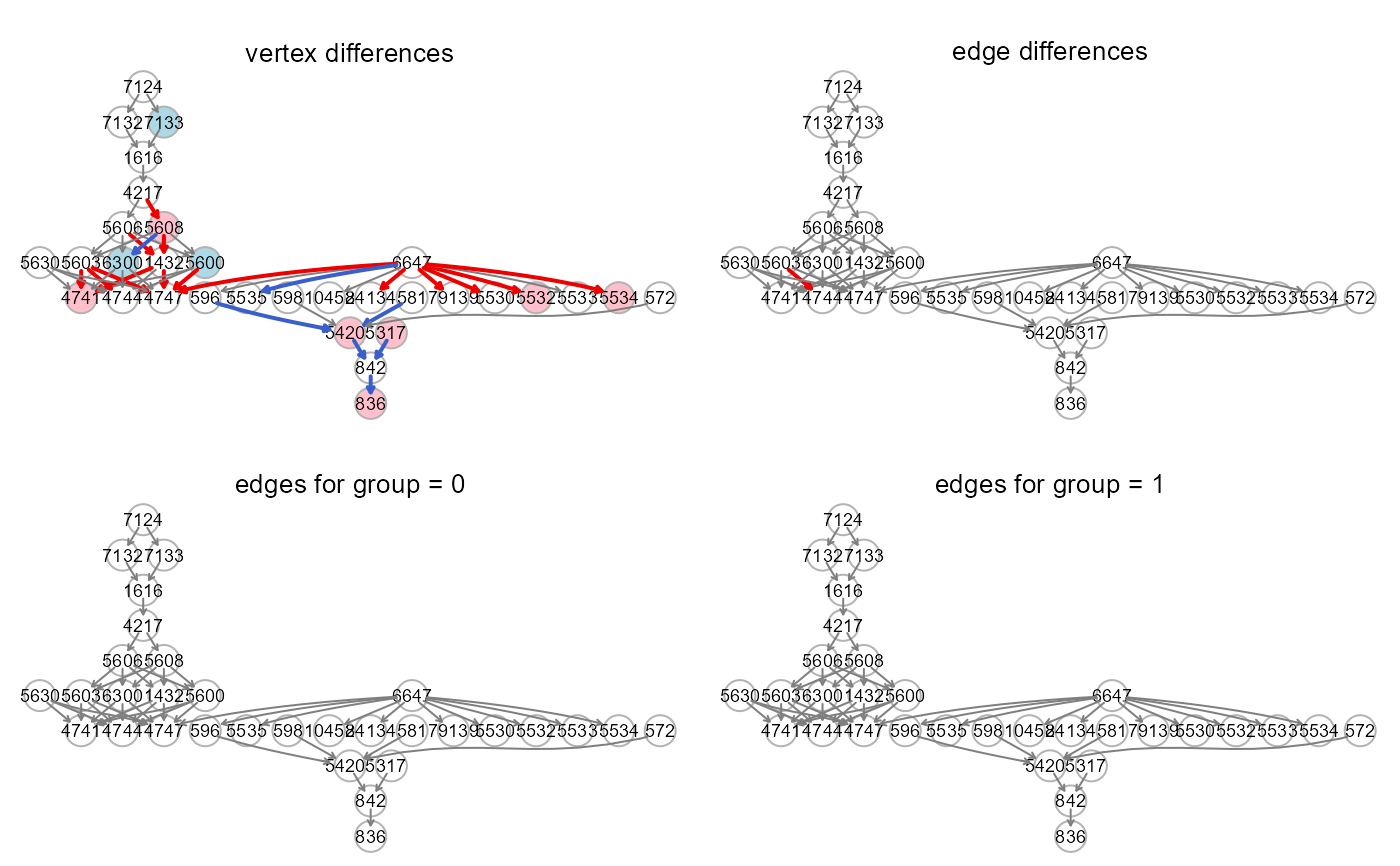
gplot(colorGraph(est = est1, g, group = x, method = "BH"),
      main = "vertex differences")
gplot(colorGraph(est = sem2$dest, g, group = NULL),
      main = "edge differences")
gplot(colorGraph(est = est20, g, group = NULL),
      main = "edges for group = 0")
gplot(colorGraph(est = est21, g, group = NULL),
      main = "edges for group = 1")

par(old.par)

# }